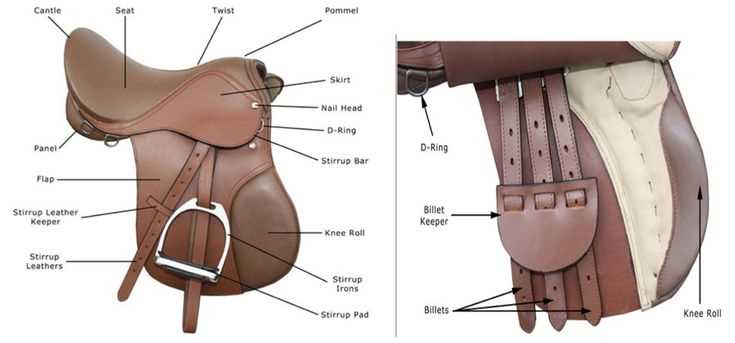
In many fields of study, visual representations of complex functions are essential for understanding their behavior. These models often involve specific features that reveal important insights into the structure of the surface being analyzed. By examining these characteristics, researchers can uncover how the surface behaves under various conditions, leading to more accurate predictions and solutions.
One of the most intriguing aspects of such surfaces is the presence of critical points. These locations serve as indicators of significant changes in the surface’s shape and can provide crucial information about the underlying function. Understanding how these points interact with other regions of the surface is key to gaining a deeper understanding of the overall model.
In this article, we will explore the fundamental components that make up these critical areas. By delving into their unique properties and how they relate to the overall structure, you will gain a clearer picture of their role in mathematical modeling and analysis.
Key Components of a Saddle Diagram

In mathematical models, certain visual elements are essential for understanding complex functions and their behaviors. These critical features provide insight into how the surface interacts with its surroundings. Recognizing these components allows for a clearer interpretation of the function’s structure and helps to identify significant characteristics that influence its overall shape.
Important Characteristics to Identify
- Critical Points: Locations where the surface reaches a peak or trough, marking transitions between different regions of behavior.
- Contours: Lines that represent regions of constant values, often used to visualize the overall shape of the model.
- Curvature: Determines the nature of the surface, showing whether it is concave or convex at various points.
- Axes of Symmetry: Imaginary lines that divide the surface into mirrored halves, helping to understand its structure and balance.
Impact of These Components on Understanding Functions
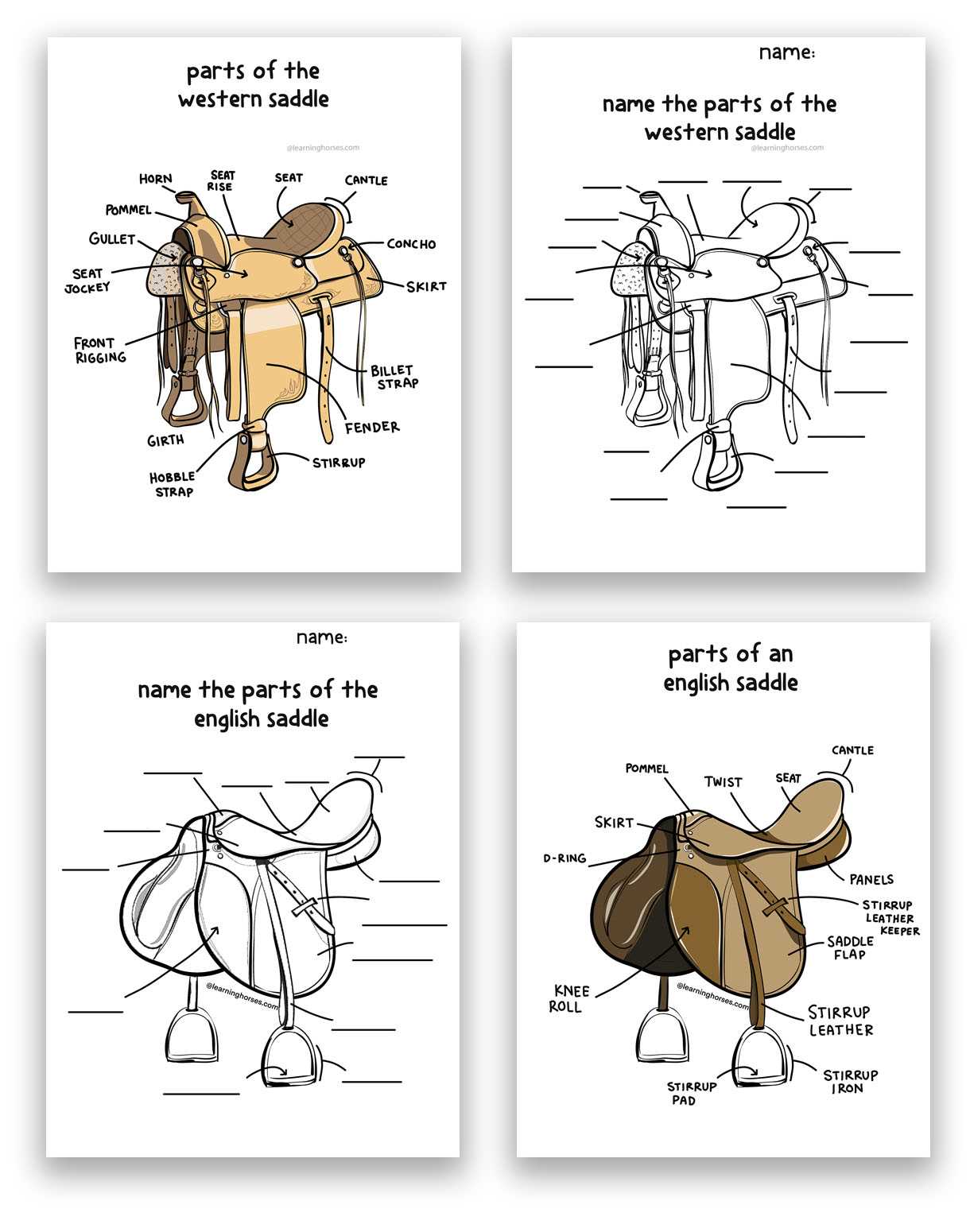
Each of these features plays a crucial role in interpreting the behavior of the model. By analyzing critical points and their surrounding contours, one can gain valuable information about the overall dynamics of the surface. Moreover, the curvature and symmetry contribute to predicting how the function will behave under different conditions, aiding in more precise calculations and conclusions.
How the Saddle Diagram is Used
Visual representations of mathematical models are crucial tools for understanding complex surfaces and their behaviors. These visualizations allow researchers and scientists to identify key features that would otherwise be difficult to detect through equations alone. By translating abstract concepts into tangible images, one can gain better insights into the structure and dynamics of a given function.
Such visual models are particularly valuable in fields like optimization and physics, where understanding the shape of a surface can lead to improved solutions and predictions. In optimization problems, for example, these models help identify points of equilibrium or stability, guiding researchers to the most efficient solutions. In physics, they can describe how different forces interact within a system, revealing areas of tension or balance.
Additionally, these models are used in machine learning and artificial intelligence to fine-tune algorithms and improve decision-making processes. By analyzing these surfaces, one can predict how adjustments will affect outcomes, enabling more accurate forecasting and better results.
Understanding the Functionality of Saddle Points
Critical points on surfaces play a significant role in determining the overall behavior of mathematical models. These points mark areas of change in the surface’s curvature, where the function switches from increasing to decreasing or vice versa. Recognizing the functionality of these specific locations is essential for understanding how a system evolves under different conditions.
Role in Optimization and Decision Making
In optimization problems, critical points often indicate solutions where a function achieves either a local maximum, minimum, or a point of equilibrium. At these points, one can identify potential optimal solutions, guiding decision-making processes. In machine learning algorithms, for example, identifying such locations helps in tuning models to minimize errors and enhance predictive accuracy.
Significance in Physical Systems
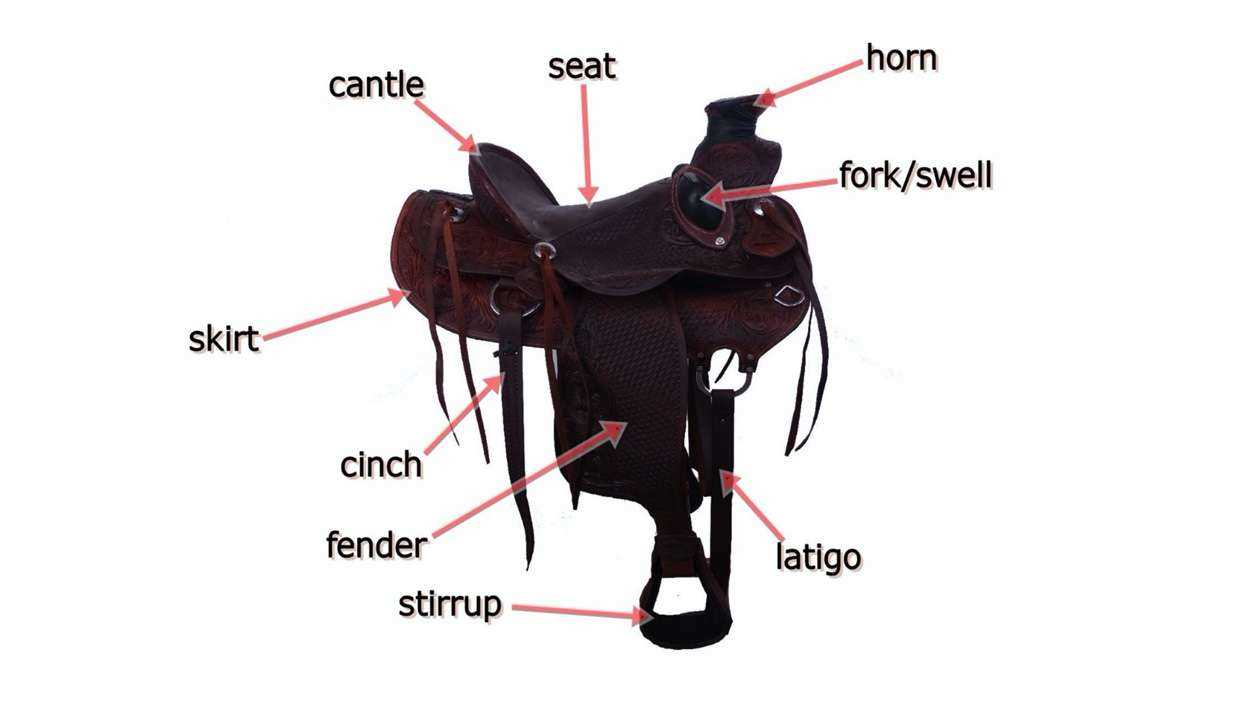
In physical systems, these key locations can represent points of stability or instability. Understanding how forces interact at these critical points can provide insight into the equilibrium of the system. For instance, in fluid dynamics, identifying where forces balance can explain the flow patterns and behavior of different fluids under various conditions.