Mathematics and physics often present complex surfaces that exhibit distinctive features. These surfaces can be studied to understand various phenomena, from optimization to fluid dynamics. A deeper exploration of these structures reveals underlying patterns that are essential for solving intricate problems.
The study of these surfaces involves identifying key regions that influence their behavior. These regions can be characterized by their curvatures and how they interact with surrounding space. Recognizing these characteristics is crucial for applying this knowledge to real-world scenarios.
Grasping the concepts behind these surfaces allows for better interpretation and prediction of their interactions. Each component plays a critical role in defining the overall structure, making it important to break them down and analyze how they contribute to the surface’s overall properties. The insights gained from this analysis can lead to advancements in both theoretical and applied fields.
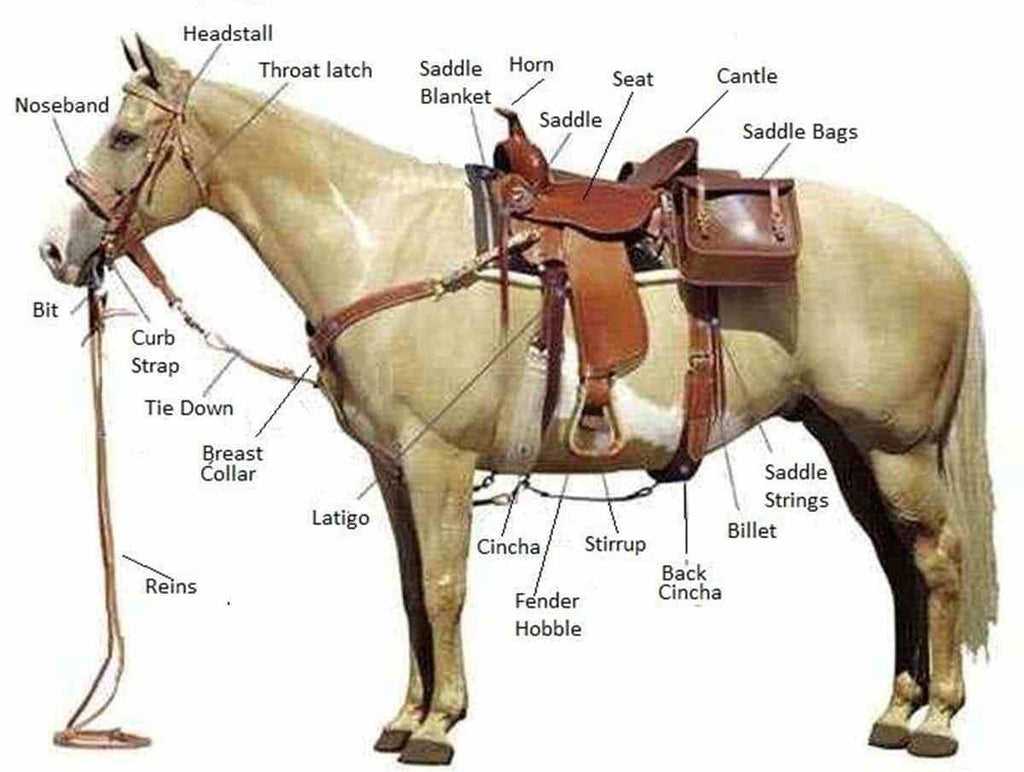
Key Elements of a Saddle Diagram
In mathematical modeling, understanding the key features of complex surfaces is essential for accurate analysis and application. These structures are often characterized by distinct points and regions that define their overall shape and behavior. Recognizing these features is crucial in determining the surface’s interaction with its environment and its role in different theoretical frameworks.
Critical Points and Curvatures
The most prominent elements of such surfaces are the critical points, where the surface reaches its maxima, minima, or points of inflection. These points are determined by the curvature of the surface in different directions. The relationship between positive and negative curvatures at these points helps in understanding how the surface behaves under various conditions, particularly in optimization and stability analysis.
Regions of Stability and Instability
Another important aspect of these surfaces is the division into regions of stability and instability. These areas are typically determined by how the surface curves around a critical point. Regions of stability tend to exhibit smooth, predictable behavior, while unstable regions may show erratic or unpredictable changes. Identifying these areas is essential for applications ranging from engineering to economics, where understanding the response of a system to various forces is critical.
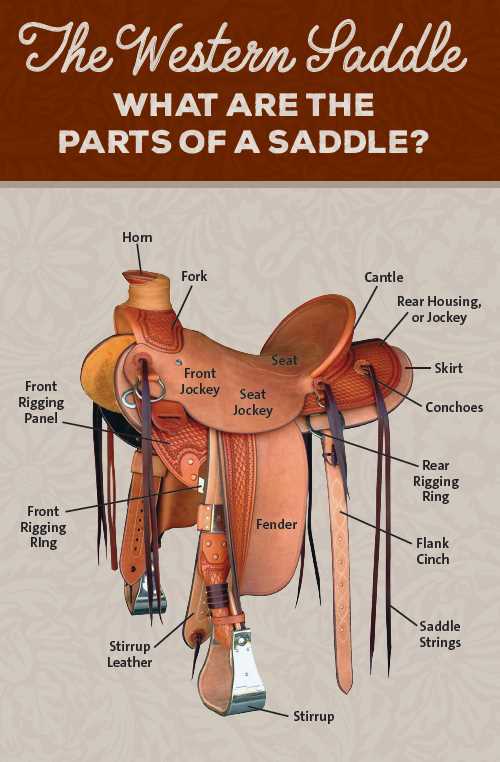
Understanding the Structure of a Saddle
Complex surfaces in mathematics often exhibit intricate shapes that can be analyzed from different perspectives. These shapes feature specific regions where the surface curves in distinct directions, creating both stable and unstable zones. Understanding the overall structure of such surfaces is crucial for grasping how they respond to external forces or changes.
Key characteristics of these surfaces include the way they curve in two different directions. One direction may show a concave shape, while the other could be convex. This interaction between opposing curvatures defines the overall geometry, leading to points of equilibrium or instability.
Exploring these structures further involves identifying the points where changes in curvature occur. These points often represent significant transitions on the surface, where the geometry shifts from one type of behavior to another. Recognizing these transitions helps in understanding how the surface interacts with its surrounding environment and predicts its response under various conditions.
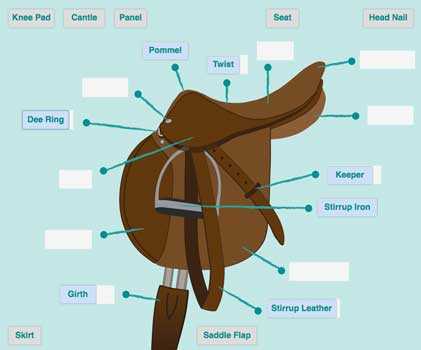
Applications of Saddle Diagrams in Science

Complex surface structures play a significant role in various scientific fields. Their ability to model systems with both stable and unstable regions makes them invaluable in understanding natural and engineered phenomena. These surfaces help researchers analyze the behavior of systems under different conditions, providing insights into everything from fluid dynamics to optimization problems.
In physics, these surfaces are often used to study equilibrium states and the forces acting on objects. For example, they can model the behavior of materials under stress, helping engineers design more resilient structures. Additionally, these surfaces are essential in understanding potential energy landscapes, which are crucial for predicting chemical reactions and phase transitions.
In economics, these mathematical models assist in analyzing market behaviors and finding optimal solutions in decision-making processes. By studying the critical points on these surfaces, economists can predict the stability of financial systems or the effects of different variables on market equilibrium.